Toffoli state を用いた Toffoli gateの実装

このエントリは、量子計算理論（森前智行著） P41の上から3つめの演習問題の回答になっています。

Toffoli gate とは

CCXゲートのことです。

真理値表は、

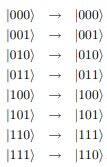
Toffoli stateとは

$$\ket{Toffoli} = \frac{1}{2} (\ket{100} + \ket{010} + \ket{001} + \ket{111})$$

 のことです。

Toffoli gateのToffoli state を用いた実装

厳密には、

Toffoli stateとクリフォード演算子を用いて、Toffoli gateを実装することができる

です。　クリフォード演算子については、直前のエントリを見てください。

以下、実装です。

全体像

実装は二段階に分かれています。

一段階目は、

$$ \ket{00} \rightarrow \ket{000}$$

$$ \ket{01} \rightarrow \ket{010}$$

$$ \ket{10} \rightarrow \ket{100}$$

$$ \ket{11} \rightarrow \ket{111}$$

にする、操作を実装します。

二段階目は一段階目で得られた状態を元にToffoli gateを実装します。

しかし、二段階目は一段階目で新たに付け加えられたqubitをコントロールビットとして、CX gateを作用させればいいだけなので、明らかです。（CXはクリフォード群に含まれているアダマールとCZをかけたらわかる。）

なので、一段階目の詳細のみ述べます。

一段階目

Toffoliのコントロールqubitになる2つのqubitを$\ket{q_{1}q_{2}}$とします。

Toffoli stateをコントロールqubitにして$\ket{q_{1}q_{2}}$にCXを作用させます。

CXのかけかたは、

Toffoli stateの一番目のqubitをコントロールqubit、$\ket{q_1}$をターゲットqubitにして作用　と

Toffoli stateの二番目のqubitをコントロールqubit、$\ket{q_2}$ ターゲットqubitにして作用

です。

$\ket{q_{1}q_{2}}$に応じて書き下しますと以下のようになります。

$$\ket{00} \otimes \ket{Toffoli} = \frac{1}{2} \left( \ket{00000} + \ket{01010} + \ket{10100} + \ket{11111} \right)$$

$$\ket{01} \otimes \ket{Toffoli} = \frac{1}{2} (\ket{01000} + \ket{00010} + \ket{11100} + \ket{10111} )$$

$$\ket{10} \otimes \ket{Toffoli} = \frac{1}{2} (\ket{10000} + \ket{11010} + \ket{00100} + \ket{01111} )$$

$$\ket{11} \otimes \ket{Toffoli} = \frac{1}{2} (\ket{11000} + \ket{10010} + \ket{01100} + \ket{00111} )$$

ここで、初めの2つのqubitを測定します。

もし、$\ket{00}$が測定されたとすると、あとの3つのqubitは、

$$ \ket{00} \rightarrow \ket{000}$$

$$ \ket{01} \rightarrow \ket{010}$$

$$ \ket{10} \rightarrow \ket{100}$$

$$ \ket{11} \rightarrow \ket{111}$$

の対応通りになっています。

もし、$\ket{01}$が測定されたら、対応は

$$ \ket{00} \rightarrow \ket{010}$$

$$ \ket{01} \rightarrow \ket{000}$$

$$ \ket{10} \rightarrow \ket{111}$$

$$ \ket{11} \rightarrow \ket{100}$$

になっています。このときは、この初めのqubitをコントロール、3つめのqubitターゲットとして、CXを作用させれば、目的のqubitを得ることができます。

他の測定の場合も、同様に測定に対して適応的に演算子をかければ目的のqubitを得ることができます。

以上で実装ができました。