効率的なstrong 量子計算シミュレータが存在しないことの証明 (Under SETH)

参考

arxiv.org

本文

Linux-kernel 4.15.0-42-generic （Ubuntu 18.04）環境でのデバイスドライバーのコンパイル

つまづきポイントを列挙します。

やり方

Makefile:

obj-m := hello.o

all:
    make -C /lib/modules/$(shell uname -r)/build M=$(shell pwd) modules
clean:
    make -C /lib/modules/$(shell uname -r)/build M=$(shell pwd) clean

hello.c

#include <linux/init.h>
#include <linux/module.h>
MODULE_LICENSE("Dual BSD/GPL");

static int hello_init(void)
{
    printk(KERN_ALERT "Hello, world\n");
    return 0;
}

static void hello_exit(void)
{
    printk(KERN_ALERT "Goodbye, cruel world\n");
}

module_init(hello_init);
module_exit(hello_exit);

を同じフォルダにいれて、makeする。

つまづきポイント一覧

・error: code model kernel does not support PIC mode

/lib/modules/$(shell uname -r)/build のMakefileに以下のリンクのパッチを当てる。(一応バックアップはしてね)
[xenial/master-next 1/1] UBUNTU: SAUCE: (no-up) disable -pie when gcc has it enabled by default

未経験の人向けに説明すると。
Makefile.patch

 Makefile | 6 ++++++
 1 file changed, 6 insertions(+)

diff --git a/Makefile b/Makefile
index dda982c..f96b174 100644
--- a/Makefile
+++ b/Makefile
@@ -608,6 +608,12 @@ endif # $(dot-config)
 # Defaults to vmlinux, but the arch makefile usually adds further targets
 all: vmlinux
 
+# force no-pie for distro compilers that enable pie by default
+KBUILD_CFLAGS += $(call cc-option, -fno-pie)
+KBUILD_CFLAGS += $(call cc-option, -no-pie)
+KBUILD_AFLAGS += $(call cc-option, -fno-pie)
+KBUILD_CPPFLAGS += $(call cc-option, -fno-pie)
+
 # The arch Makefile can set ARCH_{CPP,A,C}FLAGS to override the default
 # values of the respective KBUILD_* variables
 ARCH_CPPFLAGS :=

をさっきのMakefileと同じフォルダに入れて、

$ patch < Makefile.patch

する。

・Makefile:4: *** missing separator. Stop.

Makefileのタブでなければいけないところが半角スペースになっている。特にVScode userは気をつけてください。

・なんかよくわからないが動かない

Makefileとhello.cを置いているフォルダにある.cache.mk というファイルが悪さをしている可能性がある。make cleanしろ

これのおかげで見えてるファイルにdiffがないのに片方は動いて片方は動かないという最悪のつまりポイントが生成される。
satoru-takeuchi.hatenablog.com

Toffoli state を用いた Toffoli gateの実装

このエントリは、量子計算理論（森前智行著） P41の上から3つめの演習問題の回答になっています。

Toffoli gate とは

CCXゲートのことです。

真理値表は、

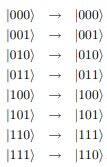
Toffoli stateとは

$$\ket{Toffoli} = \frac{1}{2} (\ket{100} + \ket{010} + \ket{001} + \ket{111})$$

 のことです。

Toffoli gateのToffoli state を用いた実装

厳密には、

Toffoli stateとクリフォード演算子を用いて、Toffoli gateを実装することができる

です。　クリフォード演算子については、直前のエントリを見てください。

以下、実装です。

全体像

実装は二段階に分かれています。

一段階目は、

$$ \ket{00} \rightarrow \ket{000}$$

$$ \ket{01} \rightarrow \ket{010}$$

$$ \ket{10} \rightarrow \ket{100}$$

$$ \ket{11} \rightarrow \ket{111}$$

にする、操作を実装します。

二段階目は一段階目で得られた状態を元にToffoli gateを実装します。

しかし、二段階目は一段階目で新たに付け加えられたqubitをコントロールビットとして、CX gateを作用させればいいだけなので、明らかです。（CXはクリフォード群に含まれているアダマールとCZをかけたらわかる。）

なので、一段階目の詳細のみ述べます。

一段階目

Toffoliのコントロールqubitになる2つのqubitを$\ket{q_{1}q_{2}}$とします。

Toffoli stateをコントロールqubitにして$\ket{q_{1}q_{2}}$にCXを作用させます。

CXのかけかたは、

Toffoli stateの一番目のqubitをコントロールqubit、$\ket{q_1}$をターゲットqubitにして作用　と

Toffoli stateの二番目のqubitをコントロールqubit、$\ket{q_2}$ ターゲットqubitにして作用

です。

$\ket{q_{1}q_{2}}$に応じて書き下しますと以下のようになります。

$$\ket{00} \otimes \ket{Toffoli} = \frac{1}{2} \left( \ket{00000} + \ket{01010} + \ket{10100} + \ket{11111} \right)$$

$$\ket{01} \otimes \ket{Toffoli} = \frac{1}{2} (\ket{01000} + \ket{00010} + \ket{11100} + \ket{10111} )$$

$$\ket{10} \otimes \ket{Toffoli} = \frac{1}{2} (\ket{10000} + \ket{11010} + \ket{00100} + \ket{01111} )$$

$$\ket{11} \otimes \ket{Toffoli} = \frac{1}{2} (\ket{11000} + \ket{10010} + \ket{01100} + \ket{00111} )$$

ここで、初めの2つのqubitを測定します。

もし、$\ket{00}$が測定されたとすると、あとの3つのqubitは、

$$ \ket{00} \rightarrow \ket{000}$$

$$ \ket{01} \rightarrow \ket{010}$$

$$ \ket{10} \rightarrow \ket{100}$$

$$ \ket{11} \rightarrow \ket{111}$$

の対応通りになっています。

もし、$\ket{01}$が測定されたら、対応は

$$ \ket{00} \rightarrow \ket{010}$$

$$ \ket{01} \rightarrow \ket{000}$$

$$ \ket{10} \rightarrow \ket{111}$$

$$ \ket{11} \rightarrow \ket{100}$$

になっています。このときは、この初めのqubitをコントロール、3つめのqubitターゲットとして、CXを作用させれば、目的のqubitを得ることができます。

他の測定の場合も、同様に測定に対して適応的に演算子をかければ目的のqubitを得ることができます。

以上で実装ができました。

How to realize Universal Quantum Computation by using of magic state.

このエントリは量子計算理論（森前智行）のP41 の上からふたつ目の演習問題の答えになっています。

Clifford group and Universal quantum computation

クリフォード群

クリフォード群Cとは、

任意の一般化パウリ行列$g \in G_n$に対して、その共役演算$UgU^\dagger$をかけてもそれが一般化パウリ行列になっているものの集合

$$ C = \{ U | \forall g \in G_n ,UgU^\dagger \in G_n \} $$

のこと

これは群の構造を持っています、中心化群（？、 一般化パウリ行列が群なので）

そして、このクリフォード群を調べてみると結局、3つの生成元でかけることがわかります。（QCQI excrsize 10.40）

その3つの生成元とは、

$$ C = \{ H, R_{\pi/2}, CZ \}$$

です。 

ここで$H$はアダマールゲート、 $R_{\theta} = \ket{0}\bra{0} + e^{i\theta}\ket{1}\bra{1}$、$CZ$はコントロールZゲート、です。

Universal quantum computation

ユニバーサルな計算はクリフォードだけではできません。できないことは明らかです。

それどころか、クリフォードだけでの計算は古典コンピュータによりシミュレーション可能です。これをGottesman-Knillの定理と呼びます。

ユニバーサルな量子計算をするには、クリフォードでないユニタリ演算子が必要になります。なんでもいいですが、例えば、

$$ R_{\pi/4}, R_{-\pi/4}$$

などがあればよいです。このどっちでもいいし、これ以外でも良いです。

Universal QC by Clifford group and Magic state

クリフォードでないユニタリ演算子がなくとも、次のMagic state$\ket{M}$が好きなだけ用意できるなら、ユニバーサルな量子計算が可能になります。

$$ \ket{M} = \cos\frac{\pi}{8}\ket{0} +\sin\frac{\pi}{8}\ket{1}$$

 以下、その証明（のようなものです）

状態$\ket{\psi} = \alpha \ket{0} + \beta\ket{1}$ に$R_{\pi/4}, R_{-\pi/4}$を作用させた状態を作り出すことができれば証明できたことになります。

つまり、

$$\ket{\psi} = \alpha \ket{0} + \beta\ket{1}$$

から出発して、

$$\alpha \ket{0} +e^{-i\pi/4}\beta\ket{1},\alpha \ket{0} +e^{i\pi/4}\beta\ket{1}$$

ができればゴールです。

$$\ket{\Psi_0} = \ket{\psi} \otimes \ket{A_{\theta}}$$

という形を考えます。

ここで、$\ket{A_{\theta}} =\ket{0} + e^{i\theta}\ket{1}$です。

$\ket{\Psi_{0}}$を$Z \otimes Z$で測定します。

すると、確率1/2で、

測定結果　＋１

$$\ket{\Psi^+_1}  = \alpha \ket{00} +\beta e^{i\theta} \ket{11}$$

測定結果　-１

$$\ket{\Psi^-_1}  = \alpha e^{i\theta}\ket{01} + \beta \ket{10}$$

がでます。

これにCX gate を適用すると

$$\ket{\Psi^+_2}  = (\alpha \ket{0} +\beta e^{i\theta} \ket{1}) \otimes \ket{0}$$

$$\ket{\Psi^-_2}  = (\alpha e^{i\theta}\ket{0} + \beta \ket{1}) \otimes \ket{1}$$

 ふたつ目のキュービットを無視します。

グローバルな位相を無視するために、$\ket{0}$の位相を揃えると、

はじめのキュービットは

$$\ket{\Psi_3}  = \alpha \ket{0} +\beta e^{\pm i\theta} \ket{1} $$

となります。

$\theta = \pi / 4$とすれば、ゴールの形になっています。

つまり、$\ket{A_{\pi /4}}$があれば、に$R_{\pi/4}, R_{-\pi/4}$の作用を実現できたことになります。

つぎに、magic stateから$\ket{A_{\pi /4}}$をつくる方法を説明します。

それは簡単で、

$$H R_{\pi / 2} \ket{M} = e^{i\pi/8} \ket{A_{\pi / 4}}$$

なので、つくれます。

以上で証明ができたことになります。 

スメール（Steven Smale）が昔、ソ連当局に拘束された話

きっかけは以下のスライドの5~8pageです。

20161005_やっぱhコボルダントでナイト☆ from matsumoring

 

特に 

モスクワでのフィールズ賞受賞 記者会見では、 アメリカの北ベトナム爆撃と ソビエトのハンガリー侵攻を 批判し当局に連行された 

 という部分に興味が湧いて、レファレンスを探したのですが、日本語ではなかなか見つかりませんでした。ので、英語でいろいろ調べました。その内容と他の調べてわかった面白スメール情報とそもそものスメール情報を以下にまとめようと思います。

いろいろ調べたところ以下の本の記述がしっかりしていました。

www.springer.com *1

大学によっては、ただで読めるかもしれません。うちの大学からは読めました。

以下の内容は基本的にこの本のP191~を参考に書かれています。

スメールとは

スティーヴン・スメイル（Stephen Smale, 1930年7月15日 - ）はアメリカの数学者。専門は微分トポロジー、力学系、数値解析。

ミシガン州フリント生まれ。ラウル・ボットの指導の下、1957年にミシガン大学でPh.D.を取得。その後、シカゴ大学、プリンストン高等研究所、カリフォルニア大学バークレー校、コロンビア大学を経てカリフォルニア大学バークレー校に戻る、1995年から香港大学教授。1962年にはコレージュ・ド・フランスの客員教授を務めた。1966年にフィールズ賞、ヴェブレン賞を受賞。

業績として、特に実力学系において、スメールの馬蹄型写像（英語版）を生み出し、双曲型構造安定な力学系（モース・スメール系）の理論を構築した。

可微分多様体上でモース関数を使用して、高次元ポアンカレ予想を解決した（この手法は4次元ポアンカレ予想にも応用された）。

(Wikipedia より)

スメールは数学にも左翼にもガチ

 微分幾何学と言ったら、「子供の頃は知性をそのまま出すとイジメられるので白痴のふりをしていた」で有名なミルナーで、微分トポロジーと言ったら「チョムスキーと双璧を成すアカデミアの二大ガチ左翼」スメール、というのがまず思い浮かびますよね。

スメールの左翼の源泉は

He had been brought up by his father with a mentality that was very anticlerical and leftist. [1]

教権反対と左翼のメンタリティを父親から仕込まれて育った。

 というように、父親きっかけだったんですね。

1966年モスクワでスメールがフィールズ賞を取る

それでは、本題の1966年にスメールがフィールズ賞を取るときどのような出来事が起こったかまとめていきます。

そこら辺について書かれた記事が下

www.abc.net.au *2

スメールはベトナム戦争には絶対反対。

スメールは1966年当時、カリフォルニア大学バークレー校にいました。UCBerkeleyといえば今も昔もリベラルの牙城ですね。

ベトナム戦争と冷戦の真っ只中だった時代に、スメールは大学でベトナム戦争の反対運動をガチでやっていました。

‘That was a very famous time in Berkeley, because that was when the free speech movement started,’ says Smale

‘I was involved in that, pretty much as a supporter to the students.’[2]

とあるように、フリースピーチムーブメントが生まれて、その中でベトナム反戦運動の学生運動をサポートしていました。

また、

Smale worked alongside colourful 1960s radical Jerry Rubin to organise a massive 35-hour anti-Vietnam war teach-in involving tens of thousands of supporters. He also attempted to stop troop trains heading to Vietnam.[2]

ジェリー・ルービンと協力して、35時間のティーチイン*3をやったりもしていたようです。

詳しくは以下の本に記述があります。

 この本によれば、ジェリー・ルービンのほうからスメールに接触したそうです。

スメール、反米活動対策委員会から召喚されるがすっぽかす

このことについては日本語の記述がありました。（注は全部引用注です）

しかし、当時*4アメリカのNSF*5の研究費を得ながら、ブラジル*6を訪問していたことが、後に、彼がバークレーでベトナム反戦運動に加わったことをきっかけに問題とされ反米活動対策委員会から召喚されることになる。事実、1968年のサイエンス誌に、ジョンソン大統領の科学補佐官が「税金を納めている一般人は、こんな数学研究はリオの浜辺の公的資金でやってくれ、と意思表示するべきだと…。」と書いているの3

http://mathsoc.jp/publication/tushin/904/nishimura.pdf(引用部は1ページ目の三段落)*7

というように、スメールは召喚されます。ですが、それをすっぽかします。

‘That's why I was eventually subpoenaed by the House of Un-American Activities,’ says Smale.

However, in a beguiling twist, Smale ducked the subpoena, because he had already left for Moscow to collect his Fields

Medal.Reporters thought they smelled a rat. A headline in The San Francisco Examiner screamed, ‘UC [University of California] Prof Dodges Subpoena, Skips US for Moscow.’ There were quiet retractions when the papers realised Smale wasn’t escaping to Moscow, but rather accepting the most prestigious medal in mathematics.

なんと、スメールは召喚を無視して、召喚のその日にモスクワに行ってしまいます。なんでモスクワかというと、フィールズ賞を受け取りにです。

上にははじめは、「教授が召喚を逃げやがって（冷戦相手の）モスクワに行ったぞ！」という記事を書いていた新聞も、スメールが数学界で最も権威のあるフィールズ賞をとりに行ったのだということを知ると掌を返したと書いてありますね。

これでなんとかなってしまうのは「アメリカ」っていう感じですかね。

スメール、フィールズ賞を受賞する

スメールはすっぽかして、モスクワに着きました。そしてフィールズ賞を受け取りました。

受賞スピーチですが、これは調べても物が出てきませんでした。ですが、ふつうに数学のことを喋っただけで、政治的なことは言わなかったのだろうと思います。

じゃあ、ソ連当局に拘束されてなかったの？と思った皆さん、安心してくださいスメールはちゃんと当局に拘束されてます。

スメール、モスクワ大学前でスピーチ "On the steps of Moscow University"

*8

スメールは賞を受け取って、会場のモスクワ大学の講堂を出るとその階段の上で記者を集めて、スピーチを行いました。

スピーチの内容が下です。

link.springer.com *9

As I wrote down my words attacking the United States from Moscow, I felt that I had to censure the Soviet Union as well*

— Stephen Smale, "On the steps of Moscow University" [4]

「アメリカ合衆国を攻撃する言葉を書いたように、私はソ連も厳しく批判しなければならない」

そのスピーチでスメールはまず、アメリカのベトナム戦争を批判しました。そして、市民が体制に抵抗することができないソ連の状況も批判しました。*10

そして、スメールはスピーチ後、

They detained Smale in order to prevent his having other contacts – treating him with all the respect due to a diplomat, and extending many a privilege to him – but they sent him away from Moscow under pretext of a long sight-seeing tour, which only came to an end when Smale had had enough and demanded to be let out of accepting other similar “courtesies”. The trip had been a long one: it was late night before he was able to return to his hotel.[1]

 車で強引に連れて行かれ、他の人間との接触を阻むため拘束されました。スメールに対する対応は、最大限の敬意を払ったものでしたが、「長い観光案内」の名目でモスクワから遠くを連れ回され、開放されたのは夜遅くでした。

ちゃんと拘束されていました！ 

このスピーチにはソ連が怒こっただけでなく、

Amidst the Cold War tensions many Americans felt the speech, in the enemy capital, was an act of treason. [5]

冷戦の最中に、敵国の首都でアメリカ批判を行うのは、自国に対する裏切り行為だとアメリカ市民は感じました。

というようにアメリカ市民も怒りました。

大変な事件ですが、この出来事についてスメールは、

‘I was in a strong position because I had just gotten the Fields Medal, and so they didn't arrest me or anything,’ says Smale.  ‘But, there were a lot of repercussions.’[4]

 フィールズ賞取ってたし逮捕は絶対されないと思ってた、と強気です。

その後

Members of Congress were outraged, and Smale's federal research grant suspended.[5]

上院議員が怒って、スメールの連邦研究資金を停止したり、

The Governor of California, president-to-be Ronald Reagan, had been following Smale’s activities and, in private, pushed to have the award-winning professor fired.  In public, Reagan called the activism at the University of California, ‘the mess at Berkeley’ and referred to Smale and his compatriots as ‘beatniks, radicals and filthy speech advocates’.

当時、カリフォルニア州知事だったレーガン*11から大学にスメールをクビにする圧力がかかったり、「ヒッピー過激クソスピーチ信奉者」と言われたりします。

それでも、スメールは30年に渡ってカリフォルニア大学バークレー校の数学教授であり続けました。

まとめ

ガチ左翼は心が強い

あと、記述が間違ってる所があったら教えてくれるとうれしいです。

参照

この本も参考にしました

 *12

*1:[1]

*2:[2]

*3:ティーチインとは大学の学生や教職員による政治問題などの討論集会

*4:1960年頃

*5:『National Science Foundation の略。アメリカ国立科学財団』by Wikipedia

*6:1960年まではアメリカとブラジルの中が悪いということはなかったと思いますが、1961年にジャニオ・クアドロスが大統領に就任してからは、アメリカとの距離を起き、ヨーロッパ諸国、東側諸国、そしてキューバ革命以来ラテンアメリカで孤立していたキューバとの関係を深めていました。その後、1964年にアメリカからの支援を受けたカステロ・ブランコ将軍がクーデターにより政権を奪取することになります。ですから、1961~1964まではアメリカとブラジルの中は悪かったろうと思います。

*7:[3]

*8: 上がシカゴ大でのスメール(1968),右下が新聞の画像、左下がモスクワでのスメール(1966)

*9:[4]

*10:

こんなことも言ってます

I believe that American military intervention in Vietnam is horrible and becomes more horrible everyday. I have great sympathy for the victims of this intervention, the Vietnamese people. However, in Moscow today, one cannot help but remember that it was only ten years ago that Russian troops were brutally intervening in Hungary and that many coura- geous Hungarians died fighting for their independence. Never could I see justification for military intervention, 10 years ago in Hungary or now in the much more dangerous and brutal American intervention in Vietnam. ... I feel I must add that what I have seen here in the discontent of the intellectuals on the Sinyavsky-Daniel trial and their lack of means of expressing this discontent, shows indeed a sad state of affairs. Even the most basic means of protest are lacking here. In all countries it is important to defend and expand the freedoms of speech and the press.

*11:「ベトナムを更地にして駐車場にすればいい」でおなじみ

*12:[5]

量子力学の数学的基礎 ヒルベルト空間と完備性

量子測定、特にインストルメントに興味がありまして勉強したいのですが、そのためには、まず、その数学的基礎について知っておかないといけない様子でした。ということで、量子力学の数学的基礎について自分用にある程度まとめていきます。

予備知識は、数学の常識と線形代数と「測度論を使えば微妙なことについてちゃんと議論できること」を知っている事、の３つです。

今回はヒルベルト空間と完備性、当分は常識が多くなると思いますが、許してください。

以下の複素数体$\mathrm{C}$を実数体$\mathrm{R}$に読み替えても成立します。量子力学では複素ヒルベルト空間しか用いないので$\mathrm{C}$で記述してあります。

ノルムと内積

定義1.0 ノルムとノルム空間

$\mathcal{H}$を$\mathrm{C}$上のベクトル空間とする。$\mathcal{H}$の任意のベクトル$\psi$に対して、数$\|\psi\|_{\mathcal{H}} \in \mathrm{R}$が対応し、以下の性質(B.1)~(B.4)が満たされるとき、$ \|\cdot\|_{\mathcal{H}} $を$\mathcal{H}$のノルム(norm)とよび、$\mathcal{H}$を$\mathrm{K}$上のノルム空間(normed vector space)あるいは、多分、前バナッハ空間(pre-Banach space)という。

 (B.1)  正値性(positiveness)　

すべての$\phi \in \mathcal{H}$に対して、$\|\phi\|_{\mathcal{H}} \geq 0$.

(B.2) 正定値性(positive-definiteness)

$\|phi\|_{\mathcal{H}} = 0$ ならば $\phi = 0$.

(B.3) 三角不等式(triangle-inequality)または劣加法性(subadditivity)

任意の$\psi, \phi \in \mathcal{H}$に対して,

$\|\psi+\phi\|_{\mathcal{H}} \leq \|\psi\|_{\mathcal{H}} + \| \phi\|_{\mathcal{H}} $

(B.4)絶対値斉次性(absolutely homogeneous)　

任意の$\psi \in \mathcal{H}$と$\alpha \in \mathrm{C}$に対して、$\|\alpha\psi\|_{\mathcal{H}} =\alpha\|\psi\|_{\mathcal{H}}$ 

定義1.1 内積と内積空間

$\mathcal{H}$を$\mathrm{C}$上のベクトル空間とする。$\mathcal{H}$の任意の二つのベクトル$\psi, \phi$に対して、数$(\psi, \phi)_{\mathcal{H}} \in \mathrm{C}$が対応し、以下の性質(H.1)~(H.4)が満たされるとき、$ (\cdot, \cdot)_{\mathcal{H}} $を$\mathcal{H}$の内積(inner product)とよび、$\mathcal{H}$を$\mathrm{K}$上の内積空間(inner product space)あるいは、前ヒルベルト空間(pre-Hilbert space)という。

(H.1)  正値性(positiveness)　

すべての$\phi \in \mathcal{H}$に対して、$(\phi,\phi)_{\mathcal{H}} \geq 0$.

(H.2) 正定値性(positive-definiteness)

$(\phi,\phi)_{\mathcal{H}} = 0$ ならば $\phi = 0$.

(H.3) 線型性(linearlity)

任意の$\psi, \phi_{1}, \phi_{2} \in \mathcal{H}$と $\alpha, \beta \in \mathrm{C}$に対して,

$(\psi,\alpha\phi_{1}+\beta\phi_{2})_{\mathcal{H}} =\alpha(\psi,\phi_{1})_{\mathcal{H}} + \beta(\psi, \phi_{2})_{\mathcal{H}} $

(H.4) 対称性(symmetry)　

任意の$\psi,\phi \in \mathcal{H}$に対して、$(\psi,\phi)_{\mathcal{H}} =(\phi,\psi)^{*}_{\mathcal{H}}$ *1

間違えやすいのですが、$(\alpha\phi_{1}+\beta\phi_{2},\psi)_{\mathcal{H}} =\alpha^{*}(\phi_{1},\psi)_{\mathcal{H}} + \beta^{*}(\phi_{2},\psi)_{\mathcal{H}} $です。また、$(\psi,\psi)_{\mathcal{H}}$は実数です。以上二つは上の定義から簡単に示せます。

内積空間上で$\|\psi\|_{\mathcal{H}} := \sqrt{(\psi,\psi)_{\mathcal{H}}}$とノルムを定義すると、これは確かにノルムになっていますね、なので内積空間はノルム空間です。

 また、"前"ヒルベルト空間 というのは何故かと言うと、完備ではないからです。前ヒルベルト空間を完備化すればヒルベルト空間になります。

完備性と反例

定義1.2 完備性

$\mathcal{H}$を$\mathrm{C}$上のベクトル空間とする。列 $\psi_{n} \in \mathcal{H}$が以下を満たすとき、それをコーシー列(cauchy sequence)、または基本列(fundamental sequence)という。

任意の$\epsilon \in \mathrm{R}$に対して、ある自然数$N$が存在し、任意の自然数$n,m > N$ に対して、 $\|\psi_{n}-\psi_{m}\| < \epsilon$を満たす

定理1.3 収束列はコーシー列である

証明略。

 定理1.3の逆は一般には偽です。そこで、以下でその例を構成します。

 前ヒルベルト空間のコーシー列で収束しない例

$\mathrm{R}$上の無限次元線形空間として以下のように定義される$l^2$を考える$$l^2 = \left\{ a = \{ a_{n} \} = (a_{1},a_{2},\cdots) \; | \; \sum_{i}^{\infty} a_{i}^{2}が有限 \right\}$$

無限次元ベクトルは、成分が無限個あるので、それを添え字の小さい方から$a_{1},a_{2},\cdots$としているわけです。数列１つ１つが$l^2$のベクトルになります。

二乗無限和が有限というのは内積を定義するために必要になってきます。

このベクトル空間で内積を(有限次元ベクトル空間の標準内積からとって)、

$$({a_{n}},b_{n})_{l^2} = \sum_{i}^{\infty}a_{i}b_{i}$$

と定義します。この内積が有限であることを示すため二乗無限和が有限という条件が必要になります。

以上から、$l^2$が少なくとも（実数）前ヒルベルト空間であることが分かりました。

$l$内の部分空間として$l_{0} \subset l^2$を以下のように定義します。

$$l_{0} = \left\{ \{a_{n}\} \; | \; a_{n}の0でない成分は有限個 \right\}$$

これは確かにベクトル空間だし、0でない成分が有限個なら無限和も有限和になるので、$l_{0}$の元は$l^2$の元である為の条件を満たします。また、「0でない成分が有限個」は「ある$N$が存在しN以上の添字の成分はすべて0」と言っても同じです。

そして、$l_{0}$は上の内積がそのまま定義できます。よって$l_{0}$が少なくとも（実数）前ヒルベルト空間であることも分かりました。

ここから、$l_{0}$のコーシー列で$l_{0}$で収束しないものを構成します。

$l_{0}$の列$\{a_{n}\}_{m} \in l_{0}$以下のように定義します。（が$l_{0}$のベクトル一個一個に付く添字で、$n$がベクトルの成分に付く添字です）

$$ \{a_{n}\}_{m} = \left\{ \begin{array}{l} a_{i} = \frac{1}{i}\;\;1 \leq i \leq m\\ a_{i} = 0 \;\; m < i \end{array} \right.$$ 

 つまり、

$$\begin{array}{l}\{a_{n}\}_{1} = (1,0,0,\cdots) \\\{a_{n}\}_{2} = (1,\frac{1}{2},0,0,\cdots)\\\vdots\\\{a_{n}\}_{m} = (1,\frac{1}{2},\cdots,\frac{1}{m},0,0,\cdots)\end{array}$$

このベクトル列は、確かにコーシー列です。なぜなら、 

$s \geq t$として、

$$\| \{a_{n}\}_{s} - \{a_{n}\}_{t} \|^{2} = \sum_{i=1}^{\infty} (a_{s,i}-a_{t,i})^2 = \sum_{i=1}^{t} (a_{s,i}-a_{t,i})^2 +\sum_{i=t+1}^{s} (a_{t,i})^2  =\sum_{i=1}^{s-t} (\frac{1}{t+i})^2$$

３つめの$=$は、第一項は$\{a_{n}\}_{s}$と$\{a_{n}\}_{t}$がsまでは同じなので0になること、第二項は$\{a_{n}\}_{s}$が添字が$s$より大きいときは0になること、から出る。最後の式は$s,t$を十分大きく取ればこれが任意の実数より小さくできることを示している。よって$\{a_{n}\}_{m}$がコーシー列になることが示されました。

$\{a_{n}\}_{m}$が$l_{0}$の中に収束するとする。その収束先を$b=\{b_{n}\} \in l_{0}$とする。$b \in l_{0}$から、ある$n_{0}$が存在して$n>n_{0}$ならば$b_{n}=0$である。また、を$\infty$に飛ばすことを意識して、$m>n_{0}$としてよい。そのもとで以下を計算する

$$\| \{a_{n}\}_{m} - b \|^{2} =  \sum_{i=1}^{n_{0}}  (a_{m,i} - b_{i})^{2} + \sum_{i=n_{0} + 1}^{m}  (a_{m,i} )^{2}$$

これが、$m \rightarrow \infty$で0に収束するはずだが、第二項は$m>n_{0}$において$\frac{1}{(n_{0}+1)^2}$より大きい。よってこれは0に収束しない。だが、これは矛盾である。

以上で例を構成することができました。

空間の定義

定義1.4 バナッハ空間

完備なノルム空間をバナッハ空間という。

定義1.5 ヒルベルト空間

完備な内積空間をヒルベルト空間という。

内積空間はノルム空間なのでヒルベルト空間はバナッハ空間です。

前ヒルベルト空間のコーシー列で収束しない例の$l^2$は実は"前"ではないヒルベルト空間です。*2そうすると、ある前ヒルベルト空間や、前バナッハ空間があったらそれを上手いこと広げてヒルベルト空間、バナッハ空間にすることができるような気がします。それは確かで、その行為を完備化といいます。

今回はここまでです。間違っているところや気になることがあったときはコメント等で教えてくれると嬉しいです✨。

*1:$*$は複素共役、つまり実数ならそのまま

*2:そこそこ容易に示せる

「打ち上げ花火、下からみるか？ 横から見るか？」を見た。よかった

映画、打ち上げ花火、下から見るか？横から見るか？ 観て来ました。
絵も深夜のテレビアニメくらいだし、
話も都合良く進み、人物も何考えてるかわからない。良かったのは音楽くらいでした。僕には退屈な映画でした。

— 奥 浩哉 (@hiroya_oku) 2017年8月18日

公開当初から、僕のTLでは上のような評価が多かったです。

他にも

• CMが作画の上澄み
• CGが酷い
• 内容がない

などいろいろ多かったのであまり期待はしていませんでしたが、院試終わったので友達を見てきました。面白かったです。

具体的な部分について

・絵が深夜のTVアニメぐらい

絵はコンディションの良いときのシャフトです。具体的には偽物語ぐらい（これでも足らない人は以下に述べる理由からシャフトを見てはいけません）

「作画の良さ」には、

・動きの良さ

・絵の綺麗さ

の二つがあります。まあ、現実は「動きの良いアニメは絵も綺麗」です。（反例はトムとジェリー）*1

この映画、普通に見てる限り動きは悪いけど絵は綺麗でした。

だからディスってるのは動きの悪さだと思うのですが、そもそも、アニメ演出には芝居派と表現派というのがいて、シャフト=新房昭之は強い表現派、表現派の旗手です。ここ数年、このやり方で円盤を売りまくってきました。そもそも、表現派というのは作画枚数制限から生まれてきたもので*2、制限された作画枚数からどれだけ客が満足する画面を作れるかを表現派は追求しています。新房に関して言えば、具体的には一枚の綺麗な絵をパンしたりパッと入れたりするやつなどです。*3そういったアニメは動きが悪いのは当然です。少ない作画で作ろうというのが、根底にあるわけですからね。

 僕の感覚としては、この絵が深夜のアニメぐらいというのは、昨今の深夜アニメの絵の綺麗になってきたからで、それはやっぱり、あのレベルの作画枚数でも大ヒットを作り出してきたシャフト=新房演出のいいところをアニメ業界全体が吸収したからだと思いますよ。

・CGが酷い

はじめ5分ぐらいの自転車などに「ンッ？」と思うシーンがありますが、他は無問題です。もしかしたら、電車のシーンでのCGに違和感を持った人もいるかもしれませんが、あれは音と映像のCGが合ってないと思えばいけます。それに、あのシーンは綺麗なシーンだったし。

・内容がない

内容が無いとは思いません。ですが、もともとの岩井俊二のドラマが45分、そこにきっちりとしたタイムリープ感*4などを付け加えても、60~75分が適正時間だったような気はします。だから薄味だったような気はする。

でも、多分「内容がない」って言ってる人はもともとのドラマをみても内容が無いって言うと思うのですが、どうでしょう？

・話も都合良く進み、人物も何考えてるかわからない

映画でもアニメでもドラマでも、任意のものをこう言って批判することができます。こういう批判は受け入れられる都合の良さはどこまでなのかを言っていただかないとなんともいえない。インターネットには本当にこればかり言っている人っています。ぐぐるとすぐ見つかります。

あと、本当に気持ちがわからないなんてことは絶対にないと思います。逆にあるあるの気持ちすぎてそこに文句をつけるのは理解できますが、原作の時代が時代なので許そう。*5

・声優

広瀬すずも菅田将暉も自然な演技で上手かった。はっきりいってむしろ宮野真守のほうが違和感が強かった。

以上、皆さんもいろいろな批判が目に入ると、映画館に行く気をなくしますが、みんなはじめ嫌いで理由を目についたものから後づけして叩くだけなので、気にせず見たいものを見て、褒めたいものを褒めましょう。

参考

アニメ表現における「芝居派」と「表現派」::サマーウォーズと化物語::クリティカルヒット

*1:動いているアニメで一時停止は汚く見えたりしますが、それは綺麗な人でも一時停止していると半目でブスだったりするのと同じです

*2:詳しくはググって

*3:ダンス イン ザ ヴァンパイアバンド とかはふつうに作ってたのに今はもうこういう演出しかしなくなりましたね

*4:もしもボックス感？

*5:1984読んで、ディストピアものあるあるすぎて創意工夫が無いというのと変わらない